Questions from the audience

Different goals. Bayesian modelling is attempting to extract a posterior distribution. This characterises the quality of every single parameter combination, relative to some user-defined measure of 'goodness-of-fit'.

So in Bayesian modelling, regions of high-posterior (the 'interesting' parameter combinations) correspond to 'clouds' in parameter space that are 'likely', given the data / objectives of the model output.

This suffers from the curse of dimensionality if you have lots of parameters.

Conversely, MinimallyDisruptiveCurves.jl extracts structure from this cloud of 'likely' parameters, without entirely characterising the cloud.

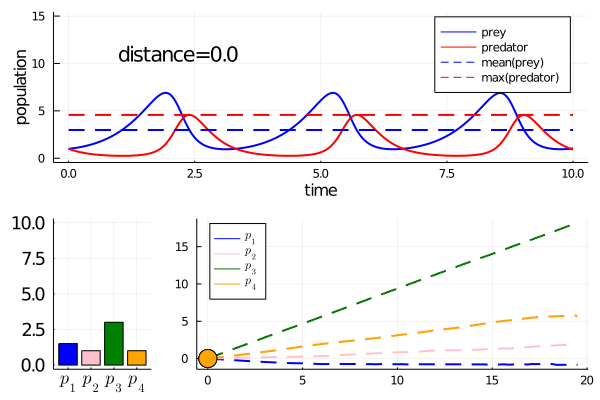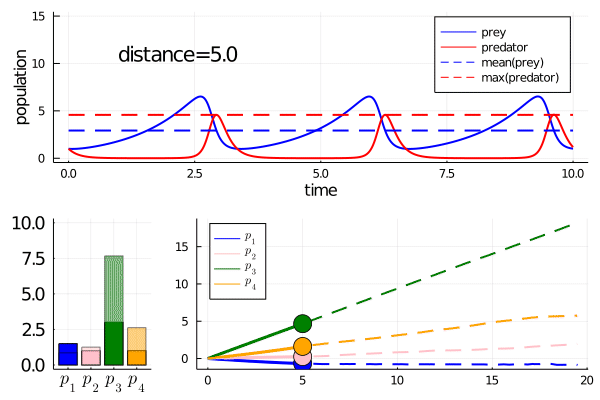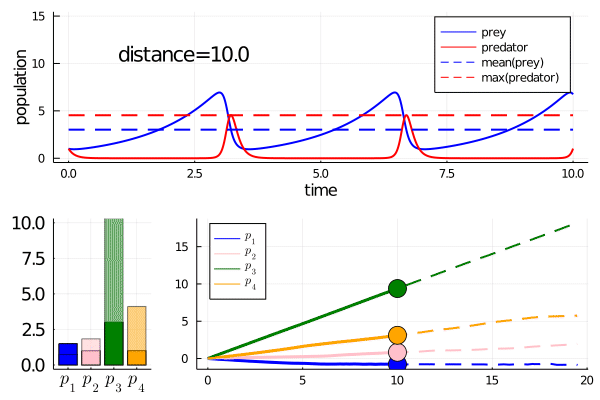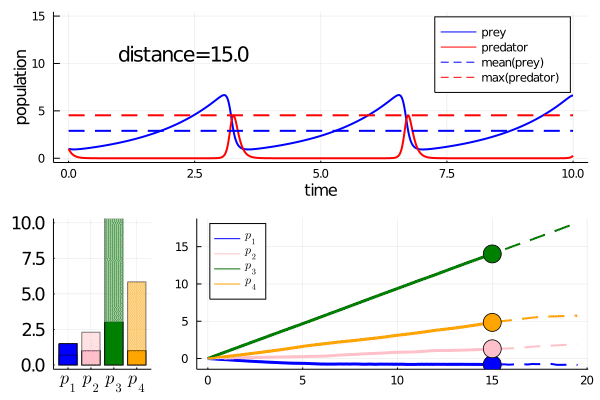
As an example, compare the output of the Bayesian inference on a Lotka Volterra example you mentioned (link here) with MinimallyDisruptiveCurves.jl:

• Turing.jl extracts regions of likely parameter values for the model (see the image after plot(chains) in the link).

• MinimallyDisruptiveCurves.jl extracts relationships between parameters over which high likelihood is maintained (see animation below)

• There is a formal correspondence between posterior / likelihood functions and minimally disruptive curves. See Raman et. al. (2017) for details.

I certainly think it could be used for social sciences! In particular, the concept of multicollinearity is very important in statistical regression analyses. This is when one regressor variable can be predicted by a linear combination of other regressor variables. It has all sorts of important practical and theoretical consequences on what can(not) be inferred from the model (see wiki link). There are various algorithmic tests to infer the existence of multicollinearity.

Now, these important consequences of multicollinearity do not come from the linearity of the relationship between regressor variables. They just come from the fact that one can be predicted by others. Why don't we test for multico-non-linearity then? Well, it's hard!

...Except this is exactly what MinimallyDisruptiveCurves.jl does!

More generally, conclusions (e.g. health risk factors in clinical population trials) are often synthesised from the parameter values of models regressed to the (e.g. clinical) data. The sensitivity analysis is local. A project I want to get off the ground is using MDC to find far away parameters that similarly match such data. For instance, if regressing my model tells me that e.g. somebody with dietary feature X has a 10% higher chance of a cardiac arrest over 10 years, can I use MDC to find different regression coefficients for the model that change this cardiac arrest probability as much as possible, while preserving model fit to the data. If I can, then the robustness of the conclusion is affected.

Why isn’t MDC.jl used so much? I guess I haven’t published a didactic paper explaining the toolbox and it’s use cases. The paper I did publish was abstract, and just arrived at the algorithm without providing an implementation. And maybe there are flaws I can’t yet see with the methodology! Either way, I’m writing a paper for this. Unfortunately, MDC is a bit of a side project for me apart from my full time job, so things go a bit slower.

Any parameter that changes a lot inside a minimally disruptive curve is unidentifiable with respect to the user defined cost function. For instance in the lotka volterra example, all parameters move quite a bit, so are effectively unidentifiable with respect to the model observation of mean prey and max predator population. The tools Villaverde et al present look for structurally unidentifiable combinations of parameters. These correspond to minimally disruptive curves that are ’non-disruptive’, i.e. the cost stays at zero. MDC can also find ‘practically unidentifiable’ combinations, unlike algebraic methods, where the cost isn't at algebraic zero, but is sufficiently small that the practical consequences are the same.

For example, if I have a reaction network with a fast timescale reaction parameter that is effectively instantaneous, I can increase this parameter to infinity with effectively zero effect on the model output. But not algebraically zero effect! So an algebraic tool wouldn’t flag the parameter as unidentifiable, whereas MDC.jl would.